Q)演習で取り扱った誤差関数を含んだ温度分布時間変化式の導出方法は？
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A) 熱伝導方程式を第三種境界条件で解いた一般解を演習で活用いたしました。
第三種境界とは熱伝達境界ともいわれ、そのほかに下記の境界条件で解いた一般解もあります。
第一種境界条件: 温度境界条件
第二種境界条件: 熱流束境界条件
講義中に伺ったご質問
A) 熱伝導方程式を第三種境界条件で解いた一般解を演習で活用いたしました。
Q)熱伝達率を稼ぐために、臨界レイノルズ数より少し上をねらうべきなのか？？
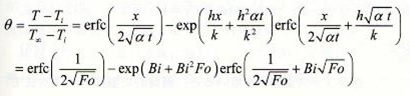
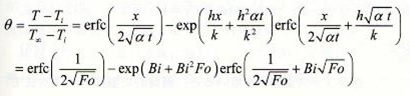
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A)冷却対象によりますが、乱流領域の熱伝達を利用する方が冷却効果が格段にあがります
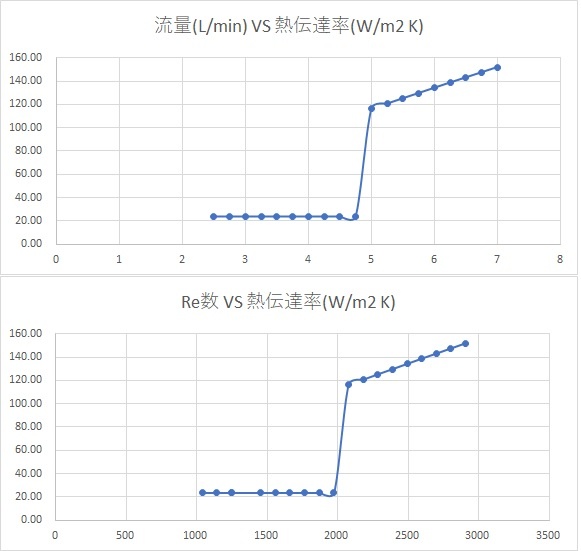
こちらの計算で示しました通り、熱伝達率は大幅にかわりますので熱伝達を促進する各種方法が勧められています。
Q)誤差関数 erf とerfcの違いは
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A) erf: 誤差関数(error function) erfc: 余誤差関数(complementary error function) と言われる関数です。
それぞれの関数の間には下記の関係が有ります。
Q)臨界レイノルズ数前後で熱伝達率は格段に変化するのか？
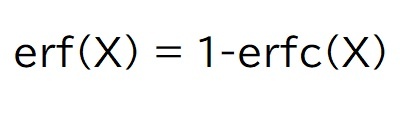
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A)流れの様相によって異なりますが一般的に2，3倍大きくなります。
水冷管内部の熱伝達率の一例を下記に示します。
横軸が流量(L/min)もしくはレイノルズ数、縦軸が熱伝達率
Q)ビオ数10以上の時に冷却対象物の表面温度が流体温度と同温となるというが、どの程度まで同温なのか？
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A) 厳密には数%未満の違いになります。
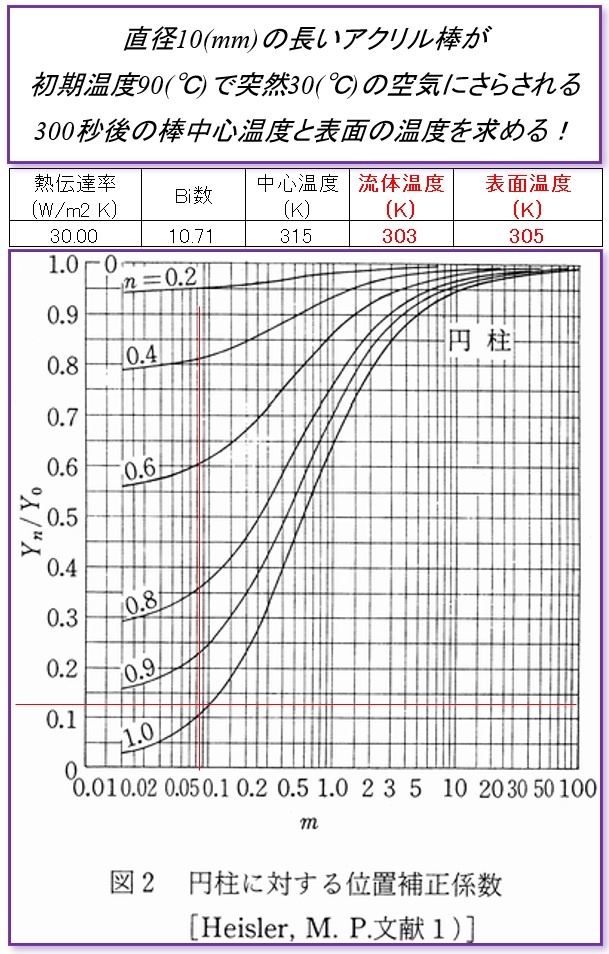
下記はプラスチック円柱表面を強制冷却した場合でビオ数が10以上の場合の結果です。
表面温度と流体温度の差は1%未満になります。
Q)熱伝達率の数式は複雑な形をしているのか？？
2022-04-25 [記事URL]
2022年4月オンライン開催セミナー中にに伺ったご質問
A) 基礎水冷空冷編での講義で詳細を説明しており、レイノルズ数、ヌセルト数という無次元数によって計算します
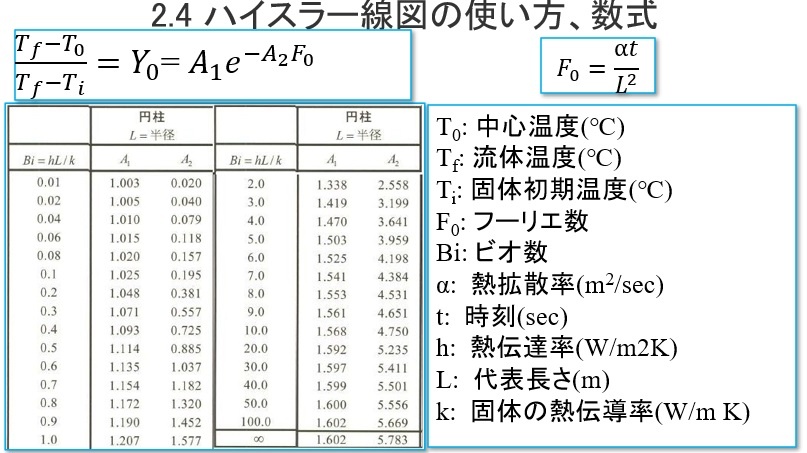
基礎温度計算編の演習では目的の温度分布時間変化を求めるための熱伝達率が与えられていますが、
実際は下記のような数式によって計算されます。
Q)ハイスラー線図の数式詳細を説明ください
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A)下記のように指数関数で表されます。
ビオ数に応じて各係数がことなります。これは熱伝導方程式を第三種境界によって解いた一般解です。
Q)熱抵抗の3種類の関係は？
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A) 熱流束、温度差、熱抵抗の関係と、各伝熱形態に相当する熱抵抗計算式を示しています。
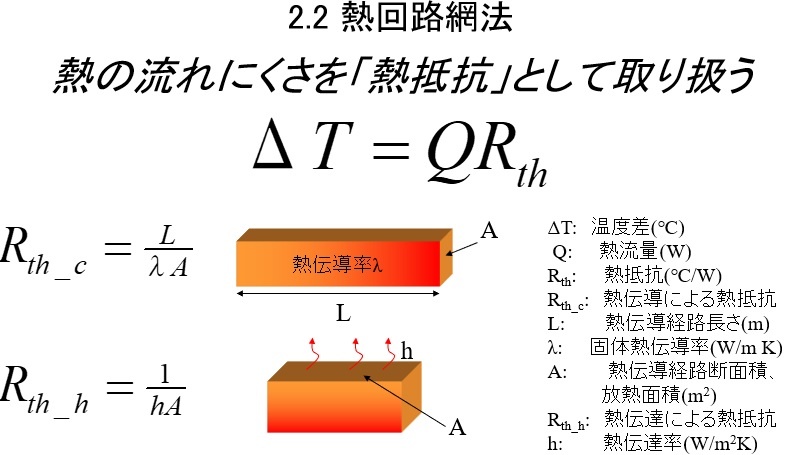
熱回路網法の基礎式と本セミナーの講義、演習で使用する熱伝導、熱伝達に相当する熱抵抗計算式を示しています。
Q)ブロアによる熱伝達率の計算シートの使い方は？
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A) ハイスラー線図演習中に仮定した熱伝達率が実現される条件を示しています。
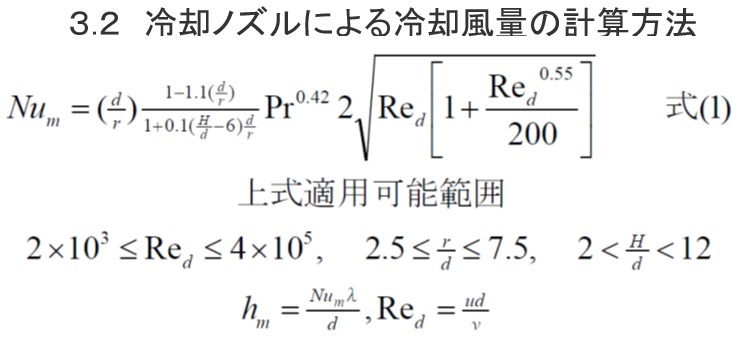
噴流熱伝達率の数式を用いて、ブロア内径、ブロアから冷却対象までの距離、冷却流量をパラメータにした熱伝達率の計算ができるエクセルシートです。
Q)固体内部の深さ方向温度分布時間変化数式は演習でどのように使われいている？？
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A) 誤差関数を用いて下記の計算式によってエクセル演習をして頂いています。
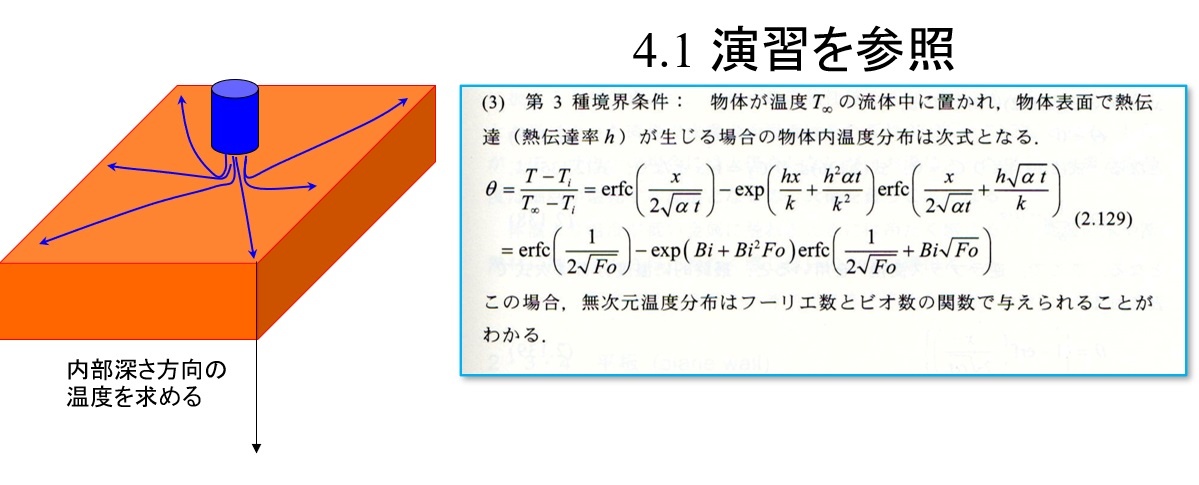
この数式は熱伝導方程式を第三種境界条件(熱伝達境界)にて解いた一般解となります。
ここで述べている
無限深さ
とは固体の反対側表面まで温度変化が伝わらない短時間の非定常現象も含みます。
Q)ビア数(ビオ数)に使用する代表長さの定義は？
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A) 円柱の場合半径、平板の場合は厚みの半分、無限固体の場合は表面からの深さです。
集中熱容量法が使える場合と、固体表面温度一定条件が適用できる場合がビア数の値によってわかります。
Q)定常熱伝導の場合に、熱伝導方程式左辺はゼロ？
[記事URL]
2022年2月オンライン開催セミナー中にに伺ったご質問
A) 熱伝導方程式左辺は温度の時間変化を意味し、定常状態ではゼロになります。
下記の式のように単純化でき、各部の温度分布は時間に依存せず一定となります。
お知らせ
2022年9月オンライン セミナー開催!
今月の予定
来月の予定
熱設計計算代行サービスも行っています
お問い合わせ
ご質問はこちらのお問い合わせフォームにご記入ください
次回公開セミナー
新着記事INFO
カテゴリーCATE
過去開催セミナ-の様子
講師の新着ブログ
対応可能地域
日本全国
アジア各国(順序不同)
中華人民共和国
中華民国(台湾)
大韓民国
タイ王国
インドネシア共和国
インド共和国
シンガポール共和国
欧米各国(順序不同)
アメリカ合衆国全域
イギリス
ドイツ連邦共和国
